介绍非晶材料的局部微观结构一直是众多研究的主题[1-8]。非常兴趣的是由几个孔形成的孔隙和簇,其负责在晶体中未观察到的不寻常的性质。一些研究人员假设在无定形固体中不可能存在大孔隙。然而,最新的模拟表明这些孔隙是相当稳定的。通过正电子湮没、小角度x射线散射和电子显微镜的实验研究已经表明,探测到的微空洞类似于晶体中的空穴。在几种真实的非晶合金中,实验发现这些“准空位”以团簇形式结合。 Chan和Elliott[9]计算了用Monte-Carlo方法构建的二氧化硅非晶态模型的孔隙分布大小。他们发现有3.1 × 1021毛孔/厘米3.半径为1.28 Å(原子半径)。类似的非晶金属模型孔隙尺寸分布的计算也发现了浓度显著的大孔隙(半径接近原子半径)[4、6和7]。对于系统CO-P和CO-B而其他[4]发现,磷原子周围的大孔的数量远大于一个周围的硼原子。此外,Co-P体系钴原子周围的大孔数大于Co-B体系钴原子周围的大孔数。简单的几何措施引入量化微观结构秩序的承担承担了结构性障碍与物理性质之间的关系。最近,它是Voronoi多面体,协调数,键合角度分布等,其可用于鉴定非晶材料的结构性偏离性。亚博网站下载然而,以往研究中所报道的孔的半径分布和围绕中心原子的孔数等孔的特征还不能完全描述孔的问题。此外,由于小模型(几千个原子)发现,仅从少数大孔中很难估计这些类空位孔的扩散作用。在本工作中,我们做了一个大的非晶模型的微观结构模拟xB1 - x提供以下资料: 一世。由孔隙形成的团簇的尺寸分布只有在大模型中才能检测到,而在非晶金属体系中还没有研究过。 2一些新的局部结构特征,提供了额外的见解,非晶态结构的系统Co-B。 3空洞状孔隙的精确浓度。 计算方法计算三种模型CO90B10,CO.81.5B18.5和co.70B30.在具有边界周期条件的立方体模拟单元中包含200,000个原子。模型的初始状态是模拟单元中所有原子的随机排列。这些模型的密度被选择为非晶合金的真实密度。然后系统被放松,直到达到新的平衡状态。最终状态是通过20,000个统计放松的步骤完成的。在[5]中,用Pak-Doyama势给出了非晶态合金CoB,所建立的模型与实验得到的偏偶分布函数(PDF)吻合较好。这种潜力有以下形式: ϕ(r) = (r-b)4+ c (r d)2+ e(1) 其中r和ϕ(r)分别为Å和eV。电位(1)被切断距离R,如表1所示。 表格1.Co-B系统的原子间作用势参数。
|
可可脂 |
-0.12812 |
-1.82709 |
1.15421 |
-2.50849 |
-0.134479 |
3.44 |
Co-B |
-0.10967 |
-1.47709 |
0.98799 |
-2.15849 |
-0.11511 |
3.09 |
b |
-0.87724 |
-2.17709 |
0.79028 |
-2.85849 |
-0.09208 |
3.79 |
每次运行后,计算PDF和局部结构特性。为了确定孔隙,我们取了模型中所有的相邻原子。如果两个原子之间的距离小于5.5 Å,就被认为是相邻的。然后是一个球体插入与这些球形原子接触。钴原子半径为1.25,硼原子半径为0.81 Å。所插入的孔可以与原子球或其他孔重叠。对于第一种情况,将插入的孔隙从体系中去除。在第二种情况下,如果这些重叠的孔隙之间的距离r和它们的半径r,则较小的孔隙将被清除1和r2(r.1< r2)满足以下条件: r1+ r2+ r < 2r2+ 0.1 r1(2) 条件(2)允许保留最大的毛孔,并从一组重叠的毛孔中去除,这些小的毛孔几乎位于一个大毛孔中。根据得到的一组孔隙,下一步是计算以下参数: 一世。模型f1(r)中所有孔隙的半径分布。 2三个项目的大小分布: -对于孤立孔隙,不与任何其他孔隙相交f2(d)。 -两个重叠的毛孔f3 (d)。 -对于超过两个重叠孔的簇f4(d)。 图1给出了这三个项目的形状,并展示了如何估计它们的直径。分别称为A型、B型和C型结构缺陷。缺陷C的中心有一个小孔,周围还有其他更小的小孔。缺陷C的直径是通过对缺陷C中所有气孔的直径进行平均计算得出的。 3围绕中心原子F5(n)的孔的数分布及其与中央孔接触的原子F6(z)的数分布。 4角度分布F7(θ),其中θ是在由四个原子具有中心创建接触的四面体角毛孔(见图1)。

|
图1.(a) a、B、c型结构缺陷的形状。(B)中心原子周围的自由体积。(c)由四个相邻原子组成的四面体内部有一个孔。这个四面体用于计算角度分布。灰色圈子 - 原子球形,白色圈子 - 孔。 |
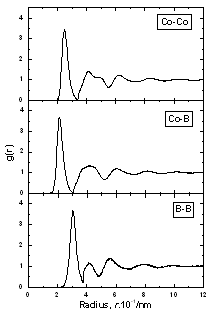
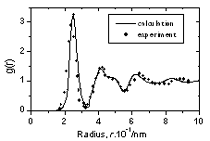
阐明局部原子排列的另一种特征是中央原子周围的自由体积,如图1所示。为了计算这个参数,在一个半径为R的中心原子中心随机插入10000个点f等于3.4 Å。这个半径对应于Co-Co对PDF的第一个最小值。中心原子周围的自由体积被确定为 v =4π(rf)3.n / (3 * 10000)(3) 其中n是模型中位于原子球外部的插入点的个数。为方便起见,非单位参数V0= 3 v / 4π(Rf)3.=n/10,000,而不是V。 结果和讨论构建模型有限公司的PDF81.5B18.5如图2所示。对于其他模型,它们的PDF也有类似的形式。一般情况下,得到的所有模型的pdf都与[7]中较小模型报告的数据接近。图3显示了计算出的总x射线PDF,并与实验数据[10]进行了比较。我们可以看到模拟可合理地再现实验数据。
|
图2.非晶型Co .的径向分布函数81.5B18.5 |
|
图3.非晶型Co .的径向分布函数81.5B18.5 |
系统的孔隙半径分布81.5B18.5如图4所示。有两个高峰。第一个高峰是0.32Å,第二个是0.52Å。半径大于0.9Å的孔数为每原子0.00474个孔。最大孔隙半径为1.38Å。如[1]所示,这些大孔隙可以与邻近的原子交换位置,因此它们在扩散过程中起到空穴的作用。这些毛孔被称为空洞状毛孔。表2列出了半径大于0.9的大腔的数量一种以及三种模型中最大毛孔的半径。如表所示2系统有限公司70B30.每个原子有0.01468个空位,毛孔,最大孔的半径等于1.66Å。对应的数值为型号Co90B10分别为0.00288和1.30 Å。该数据表明添加了小原子B破坏了基本的非晶结构,并在其中产生新的缺陷。 
图4.非晶态模型的孔隙半径分布81.5B18.5
表格2.非晶合金中每个原子的大孔洞数和最大孔洞半径。
|
每个原子的空腔数(r > 0.9) |
0.00288 |
0.00474 |
0.01468 |
模型中最大孔的半径,å |
1.30. |
1.38 |
1.66 |
图5为A、B、C型结构缺陷尺寸分布。这里未观察到两个子峰的分裂,如图4所示。因此第二个峰在半径分布f1(d)与更复杂的B型或C型缺陷有关。非晶模型Co .的分布为f2(d), f3(d)和f4(d)90B10和co.70B30.与Co相似81.5B18.5模型。缺陷A、B和C的分布峰分别位于0.62、1.28和1.90 Å处。在峰的高度上有很小的差异。它对Co的A缺陷的值70B30.,CO.81.5B18.5和co.90B10模型分别等于0.2488、0.2967和0.3229。一般情况下,富硼模型f2(d)分布较广。表3列出了由气孔形成的所有缺陷的比例。显然,随着硼浓度的增加,缺陷A的比例降低,而缺陷B和缺陷C的比例增加。随着硼浓度的增加,A缺陷的比例由0.7206降低到0.6743。相反,含两个孔以上的C缺陷的比例从0.1172增加到0.148470B30.和模型有限公司90B10.该数据还表明,随着体系中硼的加入,结构无序性增加。 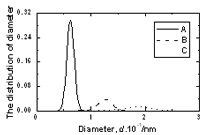
图5.研究了Co型非晶合金中A、B、C型结构缺陷的尺寸分布81.5B18.5 表格3.非晶合金中结构缺陷的比例
|
有限公司90B10 |
0.7206 |
0.1622 |
0.1172 |
有限公司81.5B18.5 |
0.7017 |
0.1703 |
0.1281 |
有限公司70B30. |
0.6743 |
0.1773 |
0.1484 |
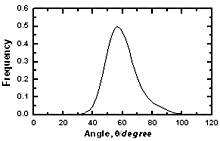
角度分布f7(θ)此角度分布为系统公司81.5B18.5如图6所示。角度分布的峰位位于60附近0这就是右四面体。在Co70B30.曲线F7的最大值(θ)位于550它比system Co .的传播范围更广81.5B18.5.相反,公司的模式90B10有更尖锐的f7峰(θ)。这意味着,如果内部有一个大的孔隙,由四个相邻原子组成且内部包含一个孔隙(图1)的四面体就会发生强烈的扭曲。
|
图6.研究了Co81.5B18.5 |
围绕中心原子的孔的数量和与孔接触的原子数分别以1至25和4至18的宽间隔分布。如图8和9所示,与硼原子相比,钴原子的分布向右移动。对于B原子和Co原子,中心原子周围的平均孔隙数分别为9和15。与晶体中的孔隙相比,这个值要大得多。因此,非晶态合金中沿间隙扩散的激活机制可能比晶体具有特定的性质。Co和B与孔洞接触的平均原子数分别为13和9。与孔的数量分布的情况进行类比,与硼原子相比,原子的数量分布也转向钴的权利。表4列出了f5(N)和f6(Z)分布的一些特征。
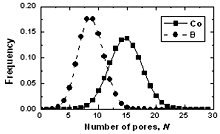
|
图7.非晶模型CO中围绕中心原子的孔的数量分布81.5B18.5 |
表格4.与孔隙接触的孔隙数和原子数的分布特征.
|
Co原子f5(N)峰的高度 |
0.1423 |
0.1379 |
0.1307 |
B原子的峰值F5(n)的高度 |
0.1817 |
0.1759 |
0.1764 |
Co原子f6(Z)峰的高度 |
0.2575 |
0.2470 |
0.2282 |
B原子峰f6(Z)的高度 |
0.3186 |
0.3141 |
0.2815 |
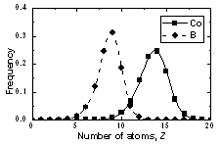
|
图8.非晶态Co模型中与孔隙接触的原子数分布81.5B18.5 |
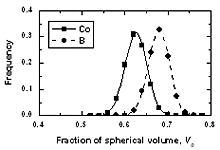
|
图9.非晶态模型中中心原子周围自由体积的分布81.5B18.5 |
图9描述了原子周围自由体积的分布。对于硼原子,它们向右移动。由图8可以看出,硼周围的自由体积分数要比钴原子大得多。大约8%的硼原子,周围的自由体积分数他们平等到0.7。很明显这些职位被称为“扩展职位”。对于钴原子,该部分对应于小于1%的浓度。而钴原子约占6%,硼原子不超过1%,游离体积小于0.5。因此它与'压缩位置'有关。 结论非晶态有限公司的结构xB100 -x具有对Pak-Doyama势的模型与实验数据很接近。这些非晶态合金中存在大量的类空孔。这种孔隙的数量随硼浓度的变化而发生强烈的变化。分析毛孔形成的不同种类簇的分布,发现所有空位样孔都涉及多于两个孔的簇。它们的近似直径比钴原子的直径大得多。因此,这种结构缺陷可以在非晶合金中发挥扩散的重要作用。角、孔数、原子数和自由体积分布的计算表明,随着体系中硼浓度的增加,非晶合金的结构会发生紊乱。结果表明,钴原子附近的原子和孔隙比硼原子周围的原子和孔隙多。相反,硼原子周围的自由体积分数大于钴原子周围的自由体积分数。此外,得到的自由体积分布也表明了非晶结构中存在“膨胀”和“压缩位置”。 确认D. K. Belashchenko教授对此表示感激承认对手稿的有用讨论和评论。 参考文献1.D. K. Belashchenko,“无序系统中的扩散机制:计算机模拟”,Uspekhi Fizicheskikh Nauk, 42(4)(1999) 297-319。 2.“二氧化硅的一阶非晶-非晶转化”,物理学报。启。, 84(2000) 4629-4532。 3.M. Scott Shell, G. Pablo, Debenedetti和Athanassios Z. Panagiotopoulos,“液态二氧化硅的分子结构有序和异常”,物理学报。Rev.E 66(2002) 011202-1 - 011202-8。 4.P. K. Hung, P. N. Nguyen和D. K. Belashchenko,“非晶合金的计算机模拟100-X.Px和有限公司81.5B18.5”,Izv。Akad。研究。金属学报,2(1998),118-121。 5.D. K. Belashchenko, V. V. huang, P. K.“非晶Co-B合金的局部结构和磁性能的计算机模拟”,J.非晶。固体,276(2000)169-180。 6.黄文强,“非晶态Ni-P合金的结构和磁性不均匀性的模拟”,J. Metast。和Nanocryst。板牙。, e-vol 9(2001) 5-20。 7.黄文伟,“B, P浓度对Co-B, Co-P合金孔隙分布影响的计算机模拟”,J. Metast。和Nanocryst。板牙。, e-vol。18(2003) 43-48。 8.“液体和非晶SiO的结构和热力学性质的计算机模拟2”,理论物理。B, 348(2004) 249-255。 9.l·陈。, S. R. Elliott,“玻璃体硅氧亚晶格间隙统计的理论研究2”,理论物理。Rev. B, 43(1991) 4423-4432。 10.P. Lamparter, E. Nold E., H. Rainer. "非晶态过渡金属-硼合金(Fe-B, Co-B, Ni-B)的x射线和中子衍射研究,中国科学(d辑),1998,15(5):527 - 534。A36 2 165 - 171。 详细联系方式 |