介绍为了延长便携式电气仪器的电池寿命,节省设备的电力消耗是一个相当重要的主题,即使对于液晶显示器(LCD)。LCD用于各种用途,特别是对于移动应用,因为其重量轻,电力低功耗。现在,诸如Zbithal Bistable Display(ZBD)之类的双稳态型LCD引起了极大的关注[1]。基于表面浮雕光栅对准的ZBD器件显示了良好的图像质量和存储能力。但是,对齐的确切机制仍然是一个可贬值的主题。Hallam和Sambles用一个拓扑对齐模型[2]进行了论证。在他们的文章中,基于液晶(LC)弹性理论[3],采用Berreman的拓扑对准模型计算了表面方位锚定能与光栅高度的函数关系。通过与光学引导模式技术的计算和实验结果的比较,发现浅振幅光栅,但不是较大的振幅光栅。他们列举了这种差异的可能原因,并描述了更全面的拓扑模型的需求。可能的矛盾原因可能是由于它们的实验准确性低。需要另一个验证实验。 有限元法(FEM)被广泛应用于求解二维和/或三维问题。可以通过有限元模拟分析液晶对准。最近,通过基于FEM的数值模拟,很好地证明了作为光栅的高度的函数的表面方位角锚固能量的饱和趋势通过数值模拟进行了良好的证明[4]。结果表明,无论是浅振幅光栅,还是深槽光栅,均与有限元计算和实验结果吻合较好。 在本文中,考虑到实际光栅表面,通过FEM研究了FEM,研究了光栅表面在表面方位角锚固能量上的依赖性。 有限元方法基于能量最小化原理的弹性理论,采用二维有限元法分析了正弦浮雕光栅表面的二维定向布置。图1是二维有限元模拟的典型结果,其中网格为30X 10个节点排列。图1中的棒代表LC导向器,LC分子的中心对应于节点。将周期性边界条件施加到左侧和左侧T侧边界。关于上边界条件,LC导向器被设置为沿玻璃基板的平行对准,这对应于散装中的导向器布置。 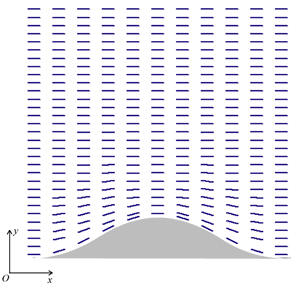
图1.来自二维有限元模拟的典型结果。Rod代表LC导演。 关于较低边界表面,假设正弦释放光栅的间距,假设正弦释放光栅,P对应于网格的一个周期。在下表面上的所有节点上,如图1所示,假设LC分子作为固定边界条件的并行对准。因为,分子垂直于脊线排列,弹性扭曲能是最大的。在一个考虑过的地区e,当θ(X,Y.)作为位置的函数(x,y)是由导演与x轴,弗兰克弹性能密度可以得到[5], 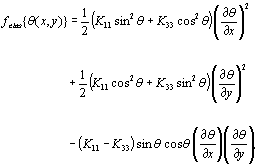 (1)
(1)
式中K11和K33为展布和弯曲变形[5]的弹性常数。有限元矩阵可以用θ(x, y)的线性近似来表示。正如过去文献[3]所描述的,如果分子与脊平行,则在表面附近不存在扭曲能。felas.表示单位面积上平行于脊的分子重新定向所释放的额外弹性能。即,在考虑区域e的弹性变形能量对应于表面方位锚定能量函数8.当F.8表达了  (2)
(2)
在哪里ΔΦ指导者与脊线之间的偏差角,表面方位锚定能量系数Aφ可以通过 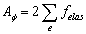 (3)
(3)
自从ΔΦ= 90˚在我们研究的条件下[2,3]。因为,如等式(2)所示,估计F年代最大时间最多ΔΦ=90˚。 为了与Berreman模型的结果进行比较,方位角锚定能量的计算公式为:[3]; 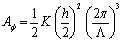 (4)
(4)
在哪里h为光栅的高度,Λ是光栅的间距和k =(k11.+ K.33.)/ 2。LC材料的弹性常数亚博网站下载K11.和K33.采用Koyama的方法进行初步测量,列于表1。 表格1。LC材料的弹性常数亚博网站下载
|
多层陶瓷- 2051 |
10.4×10-12N |
15.6×10-12N |
5CB. |
7.12×10-12N |
9.82×10-12N |
实验形成的实际释放光栅的形状将是不对称的而不是正弦的。为了研究光栅表面在表面方位角锚定能量上的依赖性,假设不对称正弦光栅和梯形格栅表面,如图2和3所示,其中参数W和D表示不对称的比率P. 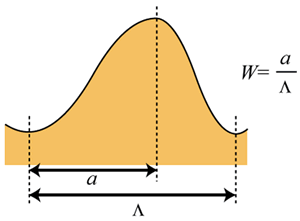
图2..本研究中计算的不对称正弦光栅的形状。 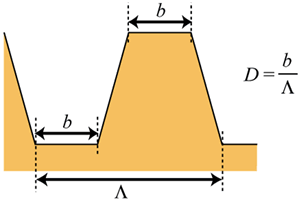
图3..本研究中计算的梯形光栅的形状。 实验我们实验中使用的光栅由光致抗蚀剂(Shipley S1830)制造。涂覆光致抗蚀剂后薄膜硼硅酸盐玻璃基板,在光致抗蚀剂膜上照射全息UV光。 图4显示了全息光的实验设置。 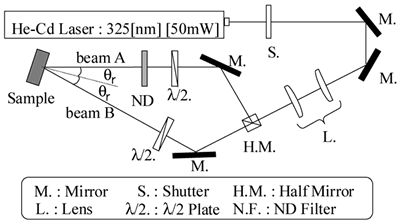
图4..全息UV光的实验设置 通过使用两个线性极化的相互连贯的CW He-CD激光束(KIMMON K3501R-G)写入光栅,其波长λ= 325nm。Λ由交叉角度决定θr在两个激光束之间,由此描述 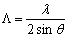 (5)
(5)
我们何时进行这些实验Λ= 2,3,4μm分别。光栅的高度由紫外激光束的强度控制。完成UV曝光后,通过原子力显微镜(Shimadzu SPM-9500J2)测量光栅的平均高度。 采用光栅基板和玻璃基板相结合的方法制备了扭曲向列型液晶样品电池,在玻璃基板上涂以聚乙烯醇(PVA)并进行预摩擦。标称细胞间隙为25μm。化学特征可能对锚定能起重要作用。特别是,表面润湿性和表面吸附对锚固能量的影响已经涉及十年。因此,采用了两种向甲型LC,一种混合物(MLC-2051,MERCK日本)和4-氰基-4'-N-戊苯基(5cb,Merck日本)。前者为本体转变型(润湿性较低)LC,后者为表面转变型(向列润湿性较高)LC[7]。 方位角锚固能量通过扭矩平衡法测量[8]。与光栅脊线的偏差角ΔΦ表示方位锚定能量Aφ由浮雕光栅引起的。这里,我们假设PVA表面处的方位角锚固相对于光栅表面相对强。[9] aφ是由体积扭矩和表面锚定扭矩之间的平衡决定的。方位锚定能量Aφ从向列相液晶的弹性理论可以得到[8] 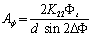 (6)
(6)
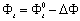 (7)
(7)
在哪里d为细胞厚度,Φt实际是扭曲和Φt0是PVA对准膜的摩擦处理方向与光栅的脊线之间的角度。在我们的实验中,与之前的纸张[8]不同,使用钨灯作为白色光源,以避免光致抗蚀剂的强吸收的错误影响。由于测量的细胞是如此厚,所以它符合Mauguin的条件[10],Φt对应于通过旋转偏振器和分析仪所找到的消光位置之间的角度。 结果与讨论图5示出了作为由Berrean模型和FEM计算的光栅高度的函数的表面方位角锚定能量的数值结果。光栅的间距应该是2,3和4μm。LC材料是MLC-2051。从图5中,在两个计算方法中发现了作为光栅高度的函数的表面方位角锚固能量的饱和趋势。虽然由FEM计算的饱和趋势比由Berreman的模型计算的更值得注意,但似乎两个计算似乎是一致的。实验结果也在图5上绘制。从我们的实验结果,高度为0.2~1.5μM光栅在两种计算中显示出良好的一致性。 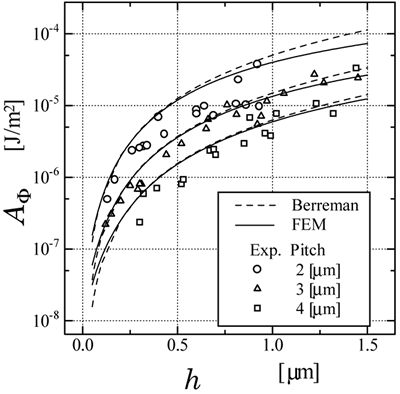
图5。表面方位角锚固能量的实验性和数值结果作为Berreman模型和FEM计算的光栅高度的函数,其中LC材料是MLC-2051。 为了验证我们的考虑,进行了另一项使用5CB的研究。为了强调光栅的明显饱和趋势不同于贝莱门原来的线性依赖关系,对光栅高度与A的平方进行了计算φ如在参考。[2]如图6所示。无论LC材料如何,都清楚地识别出大幅度光栅亚博网站下载表面的饱和趋势以及浅光栅表面的数值和实验结果之间的良好一致性。这一结果表明,弹性能比化学性质更重要,除了一些意想不到的表面条件,如光栅表面的强同向排列。 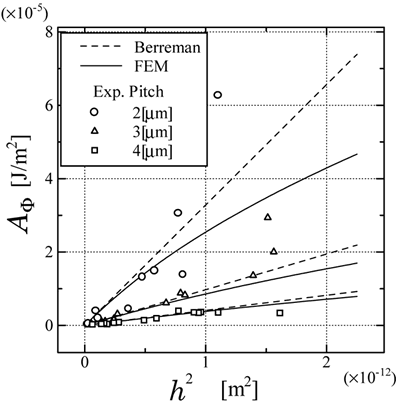
图6。表面方位角锚固能量的实验性和数值结果作为由Berrean的模型和FEM计算的光栅高度平方的函数,其中LC材料为5cb。 不对称正弦光栅可以通过全息浮雕光栅容易地获得,其中照射角设定为不对称。图7为LC材料MLC-2051中,非对称正弦光栅引起的表面方位锚定能量与有限元计算的光栅高度的函数数值结果。研究发现,非对称正弦光栅具有较强的方位锚定能量。 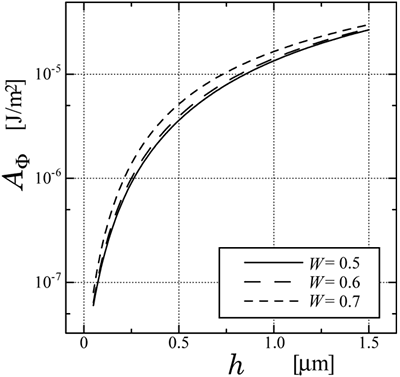
图7。用有限元方法计算了非对称正弦光栅引起的表面方位锚定能量与光栅高度的函数关系。 用电子显微镜经常可以看到,光刻胶的形状是梯形而不是矩形。因此,由光掩模工艺制造的释放光栅的形状似乎是梯形。图8示出了由梯形光栅引起的表面方位角锚定能量的数值结果,作为由FEM计算的光栅高度的函数。当光栅的形状是三角形(D = 0)时,方位角锚固能量相对较小并且取决于光栅的高度。另一方面,当光栅的形状是矩形时(D = 0.5)时,方位角锚固能量强大且不敏感到光栅的高度。这是因为我们假设刚刚在表面上方的导向器倾向于沿着表面平行地倾斜,因此导向器在矩形的侧表面附近垂直于基板对准。有限元计算得到的导向剖面如图9所示,其中D=0.4。结果表明,用有限元法计算的导向剖面是公正合理的。 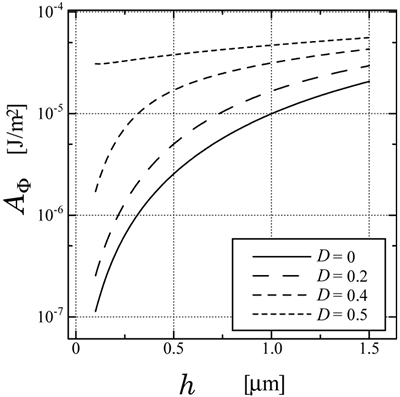
图8。由FEM计算的光栅高度的函数引起的表面方位角锚固能量的数值结果。 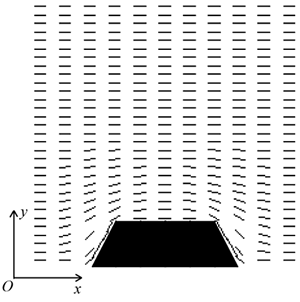
图9。用有限元法计算了导向剖面(D=0.4)。 结论它是由FEM验证的,Merreman的拓扑对准模型适用于浅光栅表面。参考报告的理论分析与实验结果之间的分歧。[2]似乎是由Berrean模型的限制而不是实验失败引起的。简单地将表面锚定公式近似于Berreman的评价水平,就可以解释这种饱和趋势,而锚定效应是由弹性而不是化学性质决定的。为了设计浮雕光栅的任意表面形状的表面方位角锚固能量,FEM可以是一个强大的工具。因为,在通过使用原子力显微镜追踪真实表面之后,所追踪的图案可以直接输入到FEM,并且可以通过FEM预测表面方位角锚固能量。 致谢我们感谢一濑先生(默克日本公司)提供LC材料。亚博网站下载本研究得到了日本科学促进会青年科学家(B)资助项目(No.15760020)的支持。亚博老虎机网登录 参考文献1。G.P.Bryan-Brown,C.V.Brown,J.C.Jones,E. L.木材,I. C. Sage,P. Brett和J. Rudin,“Groting Sixted Bistable Nematic Device”,信息显示的社会Dignt'97 Digest,(1997)P.37-40。 2。B. T. Hallam和J. R. Sambles,“凹槽深度依赖于零级光栅对齐液晶的锚固强度”,液晶,液晶,27.(2000)1207-1211。 3.王志刚,“固体表面的形状和相邻向列型液晶的排列”,物理学报。(1,28.(1972)1683-1686。 4.Y. Ohta,N.Tanaka,M.Kimura和T.Akahane,“通过有限元方法研究的光栅表面和向方液晶层之间的表面方位角锚定能”,JPN。j:。理论物理,43.(2004) 4310 - 4311。 5。F. C. Frank,《液晶:论液晶的理论》,Disc。法拉第Soc。,25(1958) 19-28. 6。K. Koyama,M. Kawaida和Askahane,“一种测定弹性常数k的方法1,K2,K3.仅限向列液晶使用均匀对齐单元格”,日本。j:。理论物理,28.(1989) 1412 - 1416。 7。S. Oka,T. Mitsumoto,M.Kimura和T. Akahane,“之间的关系年代urfaceorder和年代urface一个Zimuthal.一个nchoring.年代一个......nematicliquidcrystals“phys。rev.e,69.061711(2004)。 8。T. Akahane, H. Kaneko, M. Kimura,“测量向列型液晶表面扭转锚定强度的新方法”,日本。j:。理论物理,35.(1996) 4434 - 4437。 9。“考虑液晶分子在定向膜上吸附的方位角锚定能测量”,日本。j:。理论物理,42.(2003)6428-6433。 10。C. H. Gooch和H.A.塔瑞,“o立足p摇摆twnematicliquidcrystal年代结构与t知道一个角≤.90.°“,J. phys。,D8(1975) 1575 - 1584。 详细联系方式 |