介绍陶瓷/金属接头由于其在高温下具有稳定的力学性能和良好的耐磨、耐腐蚀和抗氧化性能,在工程领域得到了越来越广泛的应用。然而,金属和陶瓷材料性能的差异导致了界面边缘的应力奇点。此外,由于热膨胀系数的不匹配,在冷却过程中会产生较高的热残余应力。应力奇异性和热残余应力共同降低了陶瓷/金属接头的强度,使强度评估变得困难。关于陶瓷/金属接头的残余应力和强度评价已经做了大量的工作。例如,Kobayashi等[1,2]研究了Si的弯曲强度和残余应力3.N4/S45C接头及试件尺寸对弯曲强度的影响。邱等人[3]研究了残余应力和循环载荷对Si强度的影响3.N4/S45C接头。然而,由于问题的复杂性,尚未提出陶瓷/金属接头的通用评估方法。 自1959年以来,研究了界面裂纹奇异应力场的弹性解[4-9]。Rice[10]总结了该领域的工作,并建立了界面裂纹的弹性断裂力学概念。Yuuki等[11,12]基于弹性理论提出了预测陶瓷/金属接头断裂路径和强度的最大法向应力准则。由于应力奇异性,金属在裂纹尖端附近不可避免地会发生塑性变形。对于大多数陶瓷/金属接头,金属的塑性变形对陶瓷/金属接头的强度有重要影响。由于分析的复杂性,尚未基于弹塑性理论对陶瓷/金属接头的断裂路径和强度进行评估。 在本研究中,硅的四点弯曲试验3.N4/S45C接头试样具有界面裂纹。基于弹塑性分析,尝试评估断裂路径和断裂韧性。 实验样品准备图1显示了Si的几何形状和尺寸3.N4/S45C接头试样。采用厚度为60μm的银基钎焊合金(重量百分比为:Ag,71%,Cu,27%,Ti,2%)与Si之间进行连接3.N4陶瓷和S45C钢。钎焊在真空炉(2.5x10)中进行-5托尔)。炉子的温度以百分之二十的速度升高oC/min至钎焊温度850o并保持10分钟,然后以10%的速率降低oC/分钟。接合面用直径为0.25μm的金刚石粉末抛光。钎焊过程中,接触压力为0.002 MPa。 钎焊后,用直径0.1 mm的切割丝进行放电处理,产生界面裂纹。制备了4个不同裂纹长度的试件。其中2个试件裂纹长度为4.0 mm,另外2个试件裂纹长度分别为1.0 mm和2.0 mm。

|
图1所示。断裂韧性试样。 |
实验结果以0.5 mm/min的十字头速度对断裂韧性试样进行四点弯曲试验。表1显示了断裂韧性的结果。表观断裂韧性定义为:  (1) (1)
具有 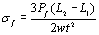 (2) (2)
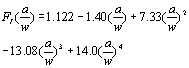 (3) (3)
Pf是断裂载荷,a是裂纹长度,w是试样宽度,t是试样高度,L2外跨与L1内部跨度。 表1。断裂韧性试验结果。
|
1 |
1 |
285.4 |
17.128 |
1.0436 |
0.9807 |
2 |
2 |
237.8 |
14.27 |
1.0530 |
1.1607 |
3. |
4 |
1649.0 |
98.95 |
1.2561 |
12.4317 |
4 |
4 |
1744.2 |
104.65 |
1.2561 |
13.1478 |
由表1可以看出,裂纹长度为4.0 mm的试件的断裂载荷高于裂纹长度为1.0和2.0 mm的试件。由于切割后残余应力将重新分布[2],较长裂纹长度的热残余应力松弛可能是一个原因。 图2显示了断裂试样的宏观观察结果。对于裂纹长度为1.0和2.0 mm的试样,裂纹扩展为Si3.N4直接从初始裂纹尖端方向约40o.对于裂纹长度为4.0mm的试样,裂纹沿界面扩展约1.0mm,然后扭结成Si3.N4在大约10的方向上o连接到接口。

(a) a = 1.0mm 
(b) a=2.0mm 
(c) a=4.0mm 
(d) a=4.0mm |
图2。断裂标本。 |
Th的振动奇异应力场界面裂纹与最大法向应力准则界面裂纹应力场的弹性解已经由william[4], Erdogan [5,6], England[7]和Sih等人[8,9]完成。发现界面裂纹尖端附近的应力场具有振荡奇异性。在原点位于裂纹尖端的极坐标下,应力场可表示为  (4) (4)
在这里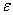 是双材料常数,可表示为
是双材料常数,可表示为 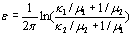 (5) (5)
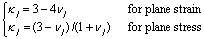 (6) (6)
在µj和vj分别是材料的剪切模量和泊松比。亚博网站下载 振荡奇异应力场的应力强度因子定义为 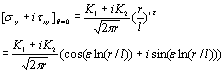 (7) (7)
在那里,l是消除振荡项维数的参考长度。通常l取整个裂纹长度的值,即l=2a。 当沿界面的应力已知时,应力强度因子可外推为:  (8) (8)
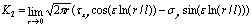 (9) (9)
Yuuki等[11,12]提出了界面裂纹断裂的最大法向应力准则。考虑到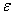 时,法向应力近似表示为
时,法向应力近似表示为  (10) (10)
在哪里 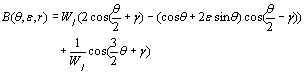 (11)
(11)
W1=e-ε(π-θ)W2=eε(π+θ)(12) 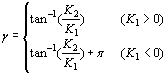 (13) (13)
最大法向应力的方向可通过以下公式确定: ∂B(θ,ε,y)/∂ θ = 0(14) 设θ0为最大法向应力方向,对应的应力强度因子可表示为: 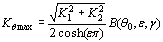 (15) (15)
断裂将沿断裂方向发生θ0当Kθmax到达K集成电路基材的价值。应注意的是,当θ0变得小于某个值,因为界面的强度通常低于基材的强度。 界面裂纹尖端弹塑性奇异应力场线性硬化材料[13]的弹塑性奇异应力场与弹性材料的弹塑性奇异应力场基本相同,其弹性常数定义为: 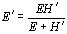 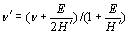 (16) (16)
式中E为杨氏模量,H为硬化系数。 因此,界面裂纹尖端的弹塑性奇异应力场与界面裂纹尖端的弹性奇异应力场基本一致。弹塑性奇异应力场的控制区域将局限在屈服区内裂纹尖端附近的一个小区域内。对于陶瓷/金属接头,考虑到硬化系数的值远小于杨氏模量的值,可以从式(16)和式(5)中发现: 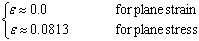 (17) (17)
有限元分析基于弹塑性应力强度因子的断裂路径和韧性的sis和评估利用ABAQUS软件在平面应力条件下进行了有限元分析。硅3.N4为弹性材料,其材料常数与温度无关,且E=289 GPa,v= 0.25和CTE = 4.2 x10-6.假设S45C钢为线性硬化材料,材料常数如表2所示[14]。无应力温度被认为是550o用于分析热残余应力。 表2。S45C的材料常数
|
E(GPa) |
206 |
206 |
201 |
197 |
192 |
187 |
183 |
v |
0.3 |
0.3 |
0.3 |
0.3 |
0.3 |
0.3 |
0.3 |
σY-(兆帕) |
375 |
348 |
333 |
309 |
280 |
241 |
193 |
H'(兆帕) |
1381 |
2056 |
2680 |
2325 |
1685 |
1026 |
687 |
CTE(10-6) |
11.71 |
12.17 |
12.63 |
13.09 |
13.55 |
14.01 |
14.47 |
为了进行比较,还进行了弹性分析。根据25的弹性常数计算oC、 双材料常数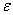 对于弹性情况为0.01588。表3列出了应力强度因子以及通过弹性分析获得的最大法向应力的方向。可以发现
对于弹性情况为0.01588。表3列出了应力强度因子以及通过弹性分析获得的最大法向应力的方向。可以发现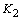 值由于残余应力大大高于
值由于残余应力大大高于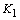 θ的值0由于残余应力几乎相同,约为70o.裂纹长度为2.0 mm的试样的最大值为Kθmax由于残余应力。K的值θmax由于断裂韧度试验中残余应力和外加应力的叠加,使断裂韧度试验与残余应力试验结果接近。
θ的值0由于残余应力几乎相同,约为70o.裂纹长度为2.0 mm的试样的最大值为Kθmax由于残余应力。K的值θmax由于断裂韧度试验中残余应力和外加应力的叠加,使断裂韧度试验与残余应力试验结果接近。 表3。根据弹性分析,应力强度因子和最大法向应力的方向。
|
a=1mm |
K1= 1.50 K2=21.05 |
25.79 |
69o |
K1= 2.5 K2=21.7 |
26.45 |
68o |
a=2mm |
K1= 0.5 K2=25.4 |
29.52 |
70o |
K1= 1.63 K2=25.42 |
30.21 |
69o |
= 4毫米 |
K1=-0.01 K2= 24.8 |
28.54 |
71o |
K1=14.0 K2=25.1 |
37.69 |
61o |
然而,弹性分析的结果显然与K值相矛盾θmax比K集成电路如果价值3.N4,约为6.0兆帕√m[15]。此外,弹性分析无法解释为什么a=4.0 mm的试样比K=1.0 mm的试样显示更高的断裂载荷θmax由于a=4.0 mm时的残余应力大于a=1.0 mm时的残余应力。 图3和图4显示了通过弹塑性分析获得的界面应力分布。图中还绘制了斜率为–0.5的线,以供参考。我们可以看到,曲线几乎平行于区域r<10内的参考线-6m、 这表明裂纹尖端附近的应力主要由弹塑性奇异应力场控制。
|
图3。沿界面的正应力分布。 |
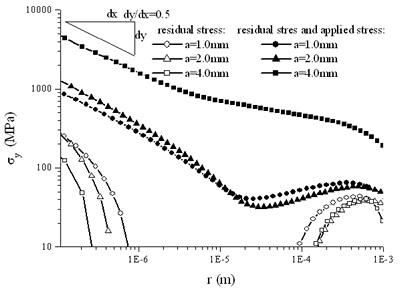
|
图4。剪切应力沿界面的分布。 |
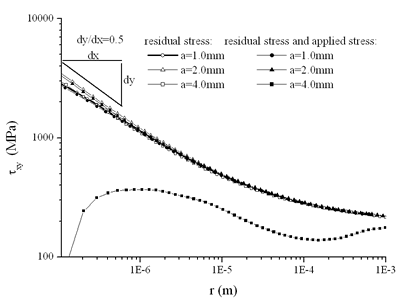
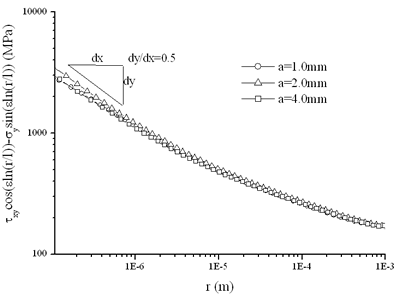
图5和图6显示了由等式(8)和等式(9)定义的未耦合组件。不同于弹性情况,这里是参考长度l承担值为1.0-6M,接近于弹塑性奇异应力场控制区域的大小。图5显示了残余应力引起的应力分布,图6显示了残余应力和施加荷载引起的应力分布。可以发现,在r<1.0范围内,曲线几乎平行于参考线-5M
|
图5。残余应力沿界面的解耦部件分布。 |
|
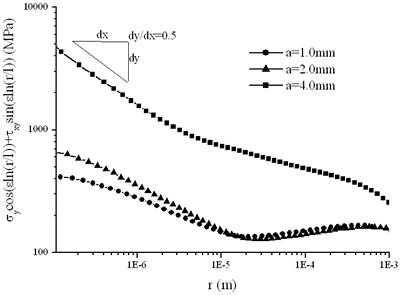
图6。试样断口处解耦构件沿界面的分布。 |
表4列出了弹塑性分析得到的应力强度因子和最大法向应力方向。可以发现Kθmax由于残余应力按a=2.0 mm、a=1.0 mm和a=4.0 mm的顺序减小。这一结果可以解释为什么裂纹长度为4.0 mm的试件比其他试件具有更高的断裂载荷。施加的载荷有减小K值的趋势2.K的降低2对于a=4.0 mm,尤其明显,θ的值0对于a=4.0 mm是33o,这比a=1.0 mm和a=2.0 mm时小得多。其中,断裂角度a=0.2 mm,与实验试样的结果a=0.2 mm一致o当a=4.0 mm的试样沿界面断裂时。的值Kθmax由于残余应力和外加应力,即断裂时的残余应力几乎相同,而不考虑裂纹长度。它们也很接近K集成电路如果价值3.N4,虽然比它少。Kobayashi等人[1]在硅的弯曲试验中发现3.N4/S45C接头的结果可分为两组,一组强度较高,另一组强度较低。低强度的一个原因被认为是陶瓷中存在裂纹,因为裂纹很容易从连接后的切割过程中的固有缺陷开始。这也可以被认为是Kθmax发生断裂时的值小于K集成电路如果价值3.N4. 表4。根据弹塑性分析得出应力强度因子和最大法向应力方向。
|
a=1mm |
K1=-0.15 K2=2.51 |
2.68 |
71o |
K1= 0.43 K2=2.50 |
3.09 |
67o |
a=2mm |
K1=-0.22 K2= 2.80 |
2.95 |
71o |
K1= 0.78 K2= 2.76 |
3.65 |
65o |
= 4毫米 |
K1=-0.30 K2= 2.45 |
2.51 |
72o |
K1=3.82 K2= 0.76 |
4.28 |
33o |
结论对硅进行了断裂韧性试验3.N4/S45C接头试样,界面裂纹长度不同。将S45C钢假定为线性硬化材料,在弹塑性分析的基础上进行了断裂路径和断裂韧性的评估。得出的结论可总结如下: •热残余应力对接头的断裂韧性有显著影响。由于残余应力的影响,裂纹长度为4.0mm的试样比裂纹长度为1.0mm和2.0mm的试样具有更高的断裂韧性。裂纹扩展成Si3.N4直接从初始裂纹尖端向40方向o当裂纹长度为1.0 mm或2.0 mm时,裂纹沿界面扩展;当裂纹长度为4.0 mm时,裂纹沿界面扩展。 •裂纹尖端附近的应力主要由弹塑性奇异应力场控制。最大限度σθ基于弹塑性奇异应力场的判据可成功地应用于断裂路径和断裂韧性值的评估。3.Kθmax残余应力引起的值按a=2.0 mm、a=1.0 mm和a=4.0 mm的顺序减小。这与a=2.0 mm、a=1.0 mm和a=4.0 mm的试样的断裂载荷顺序相同。外加应力使K值减小2.K的降低2对于a=4.0 mm的情况,θ的值是显著的0当a=4.0 mm时,明显小于a=1.0 mm和a=2.0 mm时。这与实验结果一致,即a=1.0 mm和a=2.0 mm的试样断裂角度约为40°o在界面处,a=4.0 mm试样沿界面断裂。的Kθmax各试样断裂时的数值基本相同,接近K值集成电路如果价值3.N4. 工具书类1.H. Kobayashi, Y. Arai, H. Nakamura和T. Sato,“陶瓷-金属接头的强度评估”,材料科学与工程,A143(1991) 91-102。亚博网站下载亚博老虎机网登录 2.H.Kobayashi,H.,Nakamura,A.Todoroki,W.Park,T.Koide和H.Taniai,试样切割和尺寸对陶瓷/金属接头弯曲强度的影响,JSME Trans.of JSME,A60-569(1994)65-70。 3.邱俊华,“Si3N4/S45C接头强度对残余应力的影响”,无机材料学报,13-4(1998)167-172。亚博网站下载 4.马立文,“不同介质中断层或裂缝周围的应力”,《美国地震学会通报》,49-2(1959)199-204。 5.王志强,“含裂纹粘结异种材料的应力分布”,应用力学学报。亚博网站下载动力机械。, 32(1965) 403-411。 6.F.Erdogan,“含有环形空腔的粘结异种材料中的应力分布”,J.Appl.Mech.,32(1965)8亚博网站下载29-836。 7.《不同媒介间的裂缝》,中华人民大学学报(自然科学版)。动力机械。, 32(1965) 400-407。 8.G..C.Sih和J.R.Rice,“具有裂纹的不同材料板的弯曲”,J.Appl.Mech.,31(1964)477-483。亚博网站下载 9张志强,“不同介质中裂纹的平面问题”,应用力学学报。动力机械。, 32(1965) 418-423。 10.王志强,“界面裂纹的弹性断裂力学概念”,《中国机械工程》,2006。动力机械。55(1988) 98-103。 11.r Yuuki, J.Q. Xu, Eng。打破。动力机械。,“异种材料界面开裂的应力基础判据”,41-5(1992)635-644。亚博网站下载 12.R.Yuuki,J.Q.Xu和Y.Mutoh,“基于界面断裂力学的金属/陶瓷粘结接头断裂和强度评估”,转。JSME的A60-569(1994)37-45。 13.徐志强、傅立群线性硬化材料界面边缘附近的应力场亚博网站下载”,浙江大学学报:《科学》第3-1期(2002)13-18。亚博老虎机网登录 14.N.Okabe,M.Takahashi,X.Zhu,K.Kagawa和M.Maruyama,“陶瓷/金属接头的残余应力和疲劳强度特性”,J.Soc.Mat.Sci.,日本,48-12(1999)1416-1422。 15“陶瓷/金属接头的断裂韧性评价”,国立中山大学材料科学与工程研究所硕士论文。中国机械工程学会材料力学学术会议论文集,第900-50期(1990)185-190。 详细联系方式 |